Moving Average
In some application, we need to perform moving average on input data in our design.
In the moving average for each incoming sample, we need to perform an equation like
Starting from this equation we should perform the average computation for each input sample.

If N=4, I mean
y(0) = 1/4 (x0+x1+x2+x3) y(1) = 1/4 (x1+x2+x3+x4)
At the moment, leave the 1/4 apart and focus on the add section.
y(2) = (x2+x3+x4+x5)
in other words
y(2) = y(1) + x5 - x1
This consideration can simplify the architecture of the moving average block using a simple accumulator adding the incoming sample and subtracting the outcoming as in Figure2:
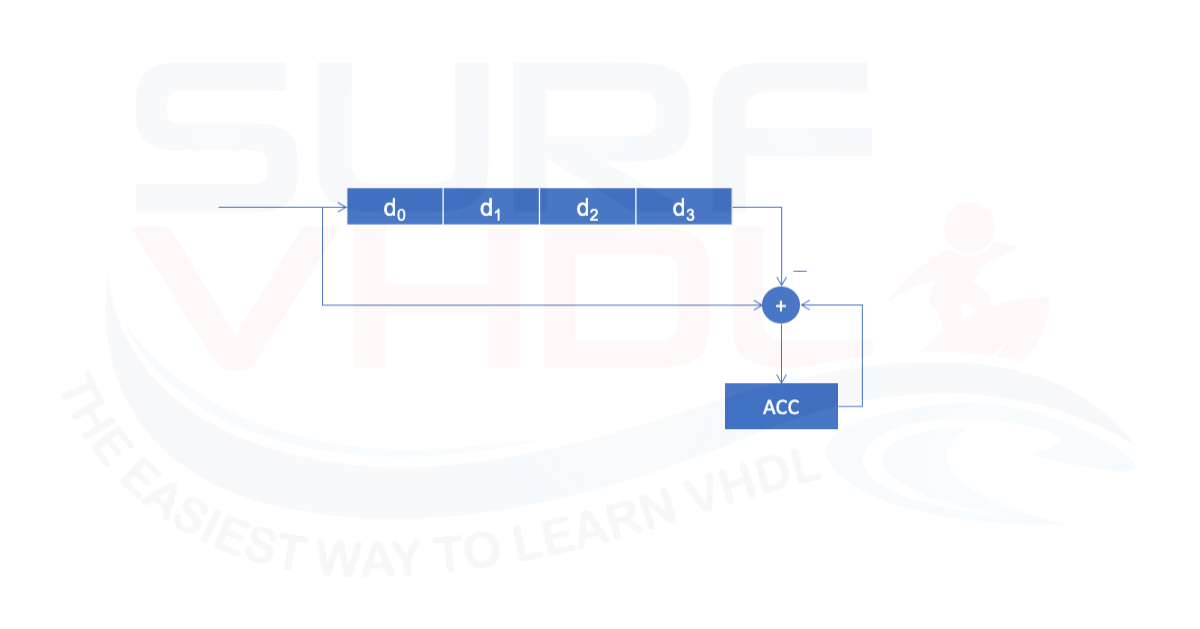
The division by N became very simple in case of N is a power of two. In fact, in this case, the division is performed simply as right shift.
In case of N is not a power of two you can refer to this post where you can learn how to implement a division by constant.
VHDL code for moving average
Here below is presented the VHDL code for the moving average architecture of Figure 2. In order to work fine, all the registers shall be in the reset state as an initial condition. This condition is implemented using a synchronous reset “i_sync_reset”.
This VHDL implementation of moving average algorithm configures the moving average length as a power of two. The generic value for moving average length is passed as log2 value so it will be simple to perform the output right shift.
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity moving_average is
generic (
G_NBIT : integer := 8;
G_AVG_LEN_LOG : integer := 2 );
port (
i_clk : in std_logic;
i_rstb : in std_logic;
i_sync_reset : in std_logic;
-- input
i_data_ena : in std_logic;
i_data : in std_logic_vector(G_NBIT-1 downto 0);
-- output
o_data_valid : out std_logic;
o_data : out std_logic_vector(G_NBIT-1 downto 0));
end moving_average;
architecture rtl of moving_average is
type t_moving_average is array (0 to 2**G_AVG_LEN_LOG-1) of signed(G_NBIT-1 downto 0);
signal p_moving_average : t_moving_average;
signal r_acc : signed(G_NBIT+G_AVG_LEN_LOG-1 downto 0); -- average accumulator
signal r_data_valid : std_logic;
begin
p_average : process(i_clk,i_rstb)
begin
if(i_rstb='0') then
r_acc <= (others=>'0');
p_moving_average <= (others=>(others=>'0'));
r_data_valid <= '0';
o_data_valid <= '0';
o_data <= (others=>'0');
elsif(rising_edge(i_clk)) then
r_data_valid <= i_data_ena;
o_data_valid <= r_data_valid;
if(i_sync_reset='1') then
r_acc <= (others=>'0');
p_moving_average <= (others=>(others=>'0'));
elsif(i_data_ena='1') then
p_moving_average <= signed(i_data)&p_moving_average(0 to p_moving_average'length-2);
r_acc <= r_acc + signed(i_data)-p_moving_average(p_moving_average'length-1);
end if;
o_data <= std_logic_vector(r_acc(G_NBIT+G_AVG_LEN_LOG-1 downto G_AVG_LEN_LOG)); -- divide by 2^G_AVG_LEN_LOG
end if;
end process p_average;
end rtl;
VHDL Moving average ModelSim simulation
In the next figures is reported a ModelSim simulation of the VHDL code implementing moving average algorithm. Figure3 is relative to input sample with continuous data enable.
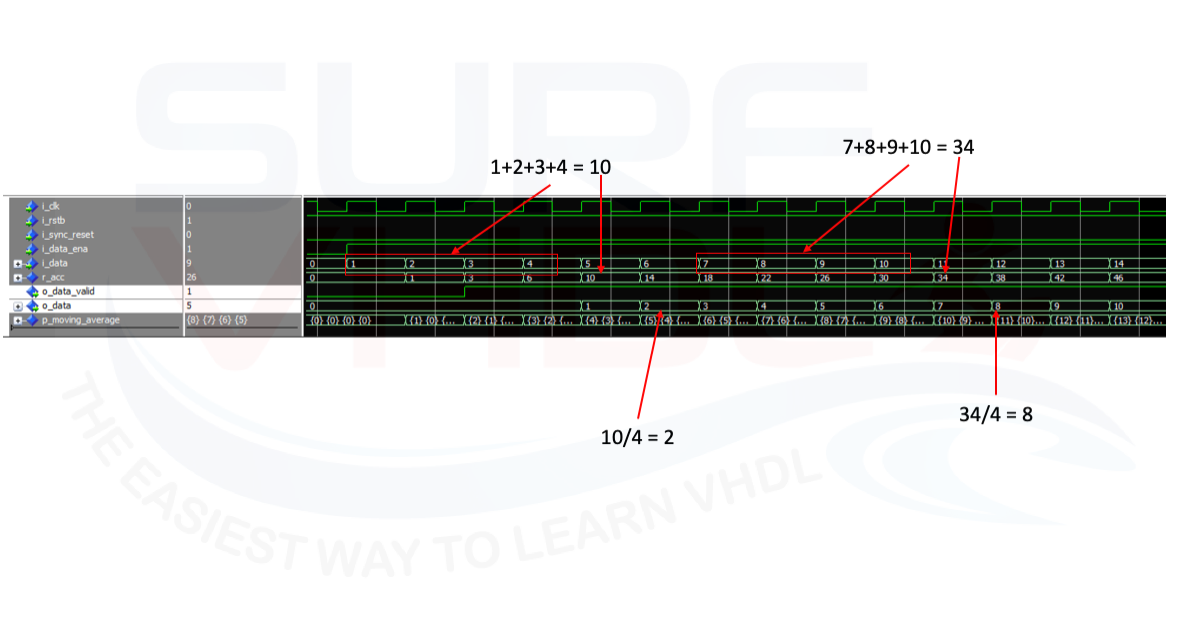
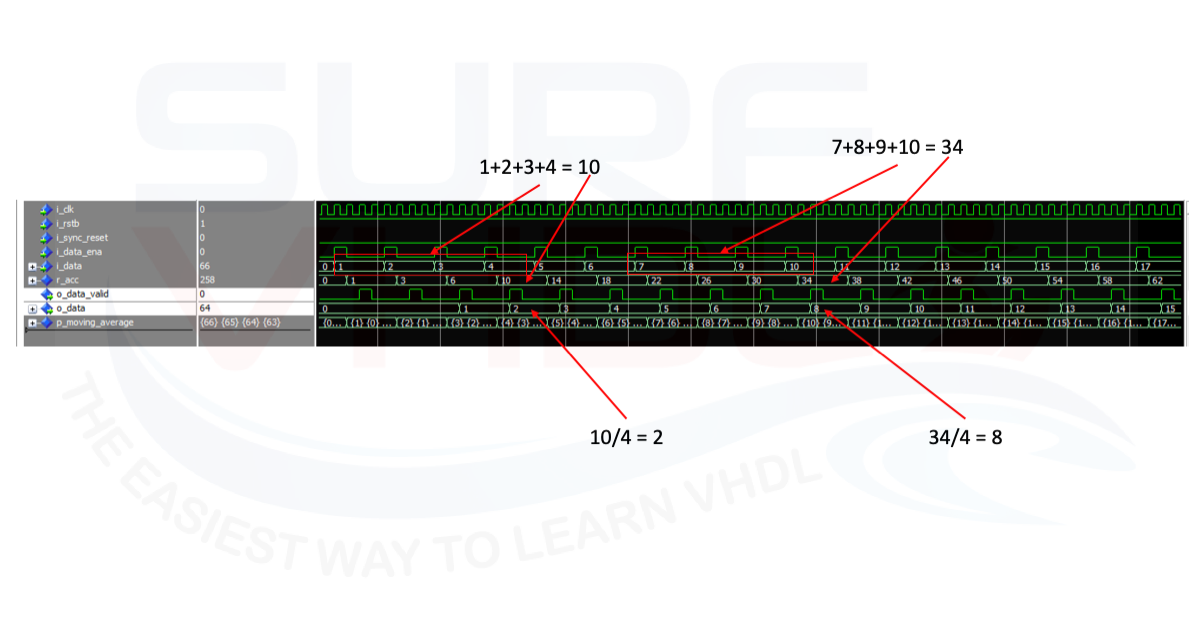
In both simulations is highlighted the moving average compute the following
1+2+3+4 = 10; => 10/4 = 2 7+8+9+10 = 34; => 34/4 = 8
Conclusion
In this post, we did address the implementation of a moving average algorithm in VHDL using a very efficient hardware structure that allows the user to implement the moving average using only a data pipe of the dimension of the moving average length and an accumulator.
The control logic is implemented as a synchronous reset that guarantees a correct initial status of the data pipe and accumulator.
In case of very long moving average length, you can adopt the FIFO implementation of the data pipe. The data pipe implemented as a FIFO is treated in this post.
In the case of FIFO implementation, an additional control logic shall be introduced to handle the initial condition of the FIFO and of the accumulator.
References
[2] https://www.mathworks.com/
[4] https://www.gnu.org/software/octave/
library IEEE;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use IEEE.NUMERIC_STD.ALL;
use ieee.std_logic_unsigned.all;
entity counter is
port(Clock: in std_logic;
reset: in std_logic;
count: out std_logic_vector(0 to 15);
dout:out std_logic);
end counter;
architecture behavioral of counter is
signal tmp: std_logic_vector(0 to 15);
begin
process (Clock, reset)
begin
if (reset=’1′) then
dout<='0';
tmp<="0000000000000000";
else if (Clock'event and Clock='1') then
tmp<=tmp + 1;
count=”XC8″&”X1068″)then
dout=”X1068″&”X11F8″)
dout<='0';
end if;
end if;
end process;
end behavioral;
——is this correct?—–plss…post the correct programm…….
It isn’t correct, but you should clarify what you want to do.
When you want to treat number it is better to use std_logic_vector(15 downto 0); instead of “to”.
I don’t understand what the code should do, for example, “dout” is std_logic so you cannot write something like
dout=”X1068″&”X11F8″
I want the vhdl code for moving average using the component based approach e.g calling multipliers and adders in main code as components…plzzz
you need to instantiate the component and connect the operand to the port of the component
moving average algorithm gives floating point values sometimes depending upon the input .How should we handle that floating numeric values and display the correct output,because in your code the outputs are in integer format?
thank you
this example is on integer values.
Basically FPGAs work on integer values, unless you use floating point, but it not the case.
Only in the last years, the FPGAs are implementing floating point block computation, but it is a particular case.
Quick Question, do I still need to divide by N on the output, N being the G_AVG_LEN_LOG or is this done on line 49?
Cheers
You don’t need to divide if you want to use the sum of all the numbers
hey, is there any method that I can find 10 numbers average instead of 4, thx for help.
just implement the memory depth 10.
In this case you cannot divide the result simply shifting to the right since 10 is not power of 2.
You can divide by 8 or 16
hello sir. sir kindly share the test bench for this code. thanks
Hi, How about making the “G_AVG_LEN_LOG” as a variable (e.g input register)?
Many thanks for the post.
I have a warning as “signal G_AVG_LEN_LOG is used in subtype-indication /type-definition” in the line of “signal r_acc : signed(G_NBIT+G_AVG_LEN_LOG-1 downto 0); — average accumulator”
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity moving_average is
generic (
G_NBIT : integer := 16);
port (
i_clk : in std_logic;
i_rstb : in std_logic;
i_sync_reset : in std_logic;
— input
i_data_ena : in std_logic;
i_data : in std_logic_vector(G_NBIT-1 downto 0);
coeff : in std_logic_vector(G_NBIT-1 downto 0);
— output
o_data_valid : out std_logic;
o_data : out std_logic_vector(G_NBIT-1 downto 0));
end moving_average;
architecture rtl of moving_average is
signal G_AVG_LEN_LOG : integer;
type t_moving_average is array (0 to 2**G_AVG_LEN_LOG-1) of signed(G_NBIT-1 downto 0);
signal p_moving_average : t_moving_average;
signal r_acc : signed(G_NBIT+G_AVG_LEN_LOG-1 downto 0); — average accumulator
signal r_data_valid : std_logic;
begin
o_data <= i_data when i_data_ena='0';
G_AVG_LEN_LOG <= to_integer(signed(coeff));
p_average : process(i_clk,i_rstb)
begin
if(i_rstb='0') then
r_acc ‘0’);
p_moving_average (others=>’0′));
r_data_valid <= '0';
o_data_valid <= '0';
o_data ‘0’);
elsif(rising_edge(i_clk)) then
r_data_valid <= i_data_ena;
o_data_valid <= r_data_valid;
if(i_sync_reset='1') then
r_acc ‘0’);
p_moving_average (others=>’0′));
elsif(i_data_ena=’1′) then
p_moving_average <= signed(i_data)&p_moving_average(0 to p_moving_average'length-2);
r_acc <= r_acc + signed(i_data)-p_moving_average(p_moving_average'length-1);
end if;
o_data <= std_logic_vector(r_acc(G_NBIT+G_AVG_LEN_LOG-1 downto G_AVG_LEN_LOG)); — divide by 2^G_AVG_LEN_LOG
end if;
end process p_average;
end rtl;
Hi, could you please help me with making the moving average length an input register or a variable, instead of a generic value.
Many thanks.
just replace the generic value with a number. The generic is a static value known at compile time. It is used to write a parametric code.
How can we design a model where n numbers are stores in n registers and arithmetic mean of the numbers in registers is calculated?
this is an FIR with an impulse response all one
http://surf-vhdl.com/how-to-implement-fir-filter-in-vhdl/
hi, i found this code about moving average filter.
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
use std.textio.all;
use ieee.std_logic_textio.all;
entity AvgFilter is
generic (
G_DATA_W :integer := 16;
G_FIL_L :integer := 4
);
port (
clk :in std_logic;
rst :in std_logic;
en :in std_logic;
iv_data :in std_logic_vector(G_DATA_W-1 downto 0);
ov_avg :out std_logic_vector(G_DATA_W-1 downto 0)
);
end entity;
architecture AvgFilter_rtl of AvgFilter is
— calculate number of bits needed to extend sum vector
function sumlog2(m :positive) return natural is
begin
for index in 1 to 30 loop
if (m <= 2**index) then
return(index);
end if;
end loop;
return(31);
end function;
signal en_reg :std_logic;
— array for storing samples
type t_arr_FilL_x_data is array (G_FIL_L-1 downto 0) of unsigned(G_DATA_W-1 downto 0);
signal a_samples :t_arr_FilL_x_data;
begin
reg: process(clk)
— to add G_FIL_L values is needed sumlog2(G_FIL_L) more bits for result
variable v_sum :unsigned(G_DATA_W+sumlog2(G_FIL_L)-1 downto 0);
begin
if rising_edge(clk) then
if rst = '1' then
en_reg <= '0';
a_samples (others => ‘0’));
v_sum := (others => ‘0’);
ov_avg ‘0’);
else
en_reg <= en;
a_samples(0) <= unsigned(iv_data);
for i in 1 to G_FIL_L-1 loop
a_samples(i) ‘0’);
if en_reg = ‘1’ then
for i in 0 to G_FIL_L-1 loop
v_sum := v_sum + resize(a_samples(i), v_sum’length);
end loop;
end if;
ov_avg <= std_logic_vector(v_sum(G_DATA_W+sumlog2(G_FIL_L)-1 downto sumlog2(G_FIL_L))); — divide by sumlog2(G_FIL_L)
end if;
end if;
end process;
end architecture;
and file dataIn.dat : 890B
0D00
0044
0048
B10E
8F1A
00A0
0A0A
But when I simulation it just only takes the top 6 values, and the average filter result is only divided by 4. can you help me explain
this one and how can i handle more than 6 values. Thanks you so much
G_FIL_L is the average length so you should get the sum of the last 4 inputs divided by 4
Thank you, i searching average filter in image processing, can you help me?
the concept is the same.
you can start from this architecture. If you need different architecture, please, post a possible architecture the community can help you
As an alternative, you can implement an exponential moving average to remove the need to store the previous values. Limiting the smoothing factor to (negative) powers of two will make it possible to use bit shifting instead of multipliers/dividers.
Mean(n) = Mean(n – 1) * (2^N – 1) / 2^N + Data(n) / 2^N = Mean(n – 1) – Mean(n – 1) >> N + Data(n) >> N
Hi thanks for your feedback.
The implementation you are suggesting the quantization error is increasing since you shift the data before adding its value Data(n) >> N