FIR Filter Introduction
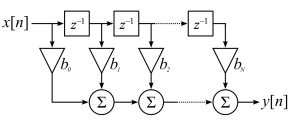
Finite Impulse Response (FIR) filters are characterized by a time response depending only on a given number of the last samples of the input signal. For a causal discrete-time FIR filter of order N, each value of the output sequence is a weighted sum of the most recent input values:
where:
- x[n] is the input signal,
- y[n] is the output signal,
- N is the filter order; a Nth-order filter has (N+1) terms on the right-hand side
- bi is the value of the impulse response at the i’th instant for 0<= i <=N of a Nth-order FIR filter. If the filter is a direct form FIR filter then is also a coefficient of the filter (see Figure1).
This computation is also known as discrete convolution.
On Wikipedia FIR web-page, you can find further information on FIR design theory.
FIR Filter Hardware Architecture
Here we want to see how to implement FIR filter architecture in FPGA or ASIC using VHDL.
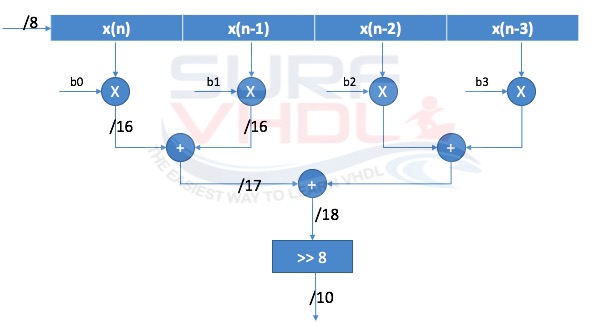
Figure 2 reports an example of 4 taps FIR direct form that can be simply coded in VHDL. In figure 2, the input x(n) and the coefficient bi are 8-bits signed.
After the filter coefficients multiplication, the multiplier output dynamic will be an 8+8=16 bit.
In fact, when you multiply two numbers of N-bit and M-bit the output dynamic of the multiplication result is (N+M)-bits.
When you perform addition, the number of bit of the result will be incremented by 1. The FIR filter design architecture of figure 2 can be easily extended to a length greater than 4.
FIR Filter Design VHDL Code
Here below is reported the VHDL code for the FIR filter design of figure 2. The VHDL code implements a low pass FIR filter with 4 taps, 8-bit input, 8-bit coefficient.
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
entity fir_filter_4 is
port (
i_clk : in std_logic;
i_rstb : in std_logic;
-- coefficient
i_coeff_0 : in std_logic_vector( 7 downto 0);
i_coeff_1 : in std_logic_vector( 7 downto 0);
i_coeff_2 : in std_logic_vector( 7 downto 0);
i_coeff_3 : in std_logic_vector( 7 downto 0);
-- data input
i_data : in std_logic_vector( 7 downto 0);
-- filtered data
o_data : out std_logic_vector( 9 downto 0));
end fir_filter_4;
architecture rtl of fir_filter_4 is
type t_data_pipe is array (0 to 3) of signed(7 downto 0);
type t_coeff is array (0 to 3) of signed(7 downto 0);
type t_mult is array (0 to 3) of signed(15 downto 0);
type t_add_st0 is array (0 to 1) of signed(15+1 downto 0);
signal r_coeff : t_coeff ;
signal p_data : t_data_pipe;
signal r_mult : t_mult;
signal r_add_st0 : t_add_st0;
signal r_add_st1 : signed(15+2 downto 0);
begin
p_input : process (i_rstb,i_clk)
begin
if(i_rstb='0') then
p_data <= (others=>(others=>'0'));
r_coeff <= (others=>(others=>'0'));
elsif(rising_edge(i_clk)) then
p_data <= signed(i_data)&p_data(0 to p_data'length-2);
r_coeff(0) <= signed(i_coeff_0);
r_coeff(1) <= signed(i_coeff_1);
r_coeff(2) <= signed(i_coeff_2);
r_coeff(3) <= signed(i_coeff_3);
end if;
end process p_input;
p_mult : process (i_rstb,i_clk)
begin
if(i_rstb='0') then
r_mult <= (others=>(others=>'0'));
elsif(rising_edge(i_clk)) then
for k in 0 to 3 loop
r_mult(k) <= p_data(k) * r_coeff(k);
end loop;
end if;
end process p_mult;
p_add_st0 : process (i_rstb,i_clk)
begin
if(i_rstb='0') then
r_add_st0 <= (others=>(others=>'0'));
elsif(rising_edge(i_clk)) then
for k in 0 to 1 loop
r_add_st0(k) <= resize(r_mult(2*k),17) + resize(r_mult(2*k+1),17);
end loop;
end if;
end process p_add_st0;
p_add_st1 : process (i_rstb,i_clk)
begin
if(i_rstb='0') then
r_add_st1 <= (others=>'0');
elsif(rising_edge(i_clk)) then
r_add_st1 <= resize(r_add_st0(0),18) + resize(r_add_st0(1),18);
end if;
end process p_add_st1;
p_output : process (i_rstb,i_clk)
begin
if(i_rstb='0') then
o_data <= (others=>'0');
elsif(rising_edge(i_clk)) then
o_data <= std_logic_vector(r_add_st1(17 downto 8));
end if;
end process p_output;
end rtl;
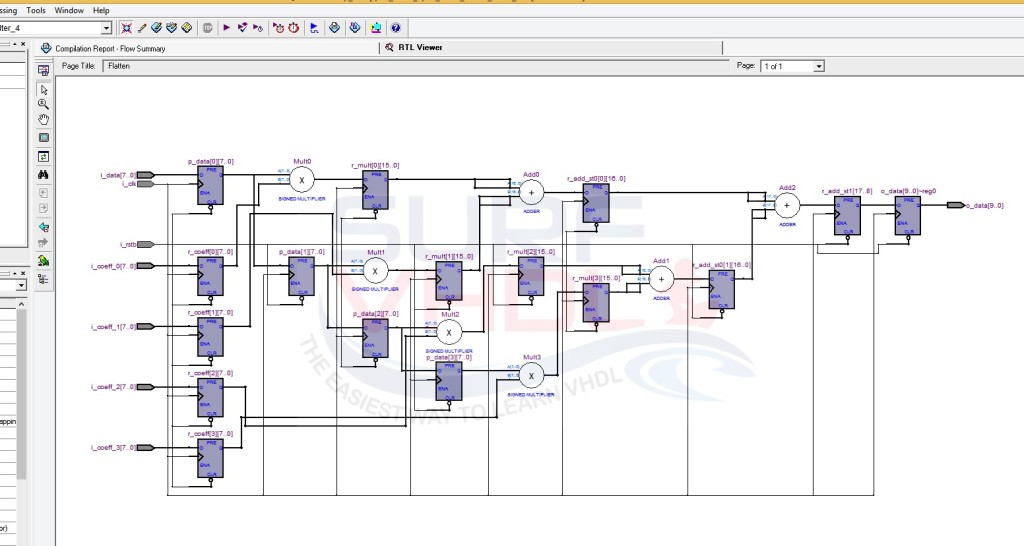
The FIR filter is implemented fully pipelined, in fact, there is a registration stage at the output of each multiplication or addition.
The output dynamic of the FIR filter is 10-bit, i.e. is not fully dynamic output.
The VHDL code of the FIR filter can be implemented either in ASIC or in FPGA. The implementation should be guarantee full speed for the FIR filter.
Figure 3 shows RTL viewer of Altera Quartus II for the FIR filter VHLD example code above
If you appreciated this post, please help us to share it with your friend.
[social_sharing style=”style-7″ fb_like_url=”https://surf-vhdl.com/how-to-implement-fir-filter-in-vhdl” fb_color=”light” fb_lang=”en_US” fb_text=”like” fb_button_text=”Share” tw_lang=”en” tw_url=”https://surf-vhdl.com/how-to-implement-fir-filter-in-vhdl” tw_button_text=”Share” g_url=”https://surf-vhdl.com/how-to-implement-fir-filter-in-vhdl/” g_lang=”en-US” g_button_text=”Share” linkedin_url=”https://surf-vhdl.com/how-to-implement-fir-filter-in-vhdl” linkedin_lang=”en_US” alignment=”center”]
If you need to contact us, please write to: surf.vhdl@gmail.com
We appreciate any of your comment, please post below:
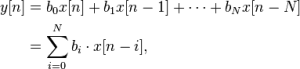
very nice , just great , please so on
Isn’t your code a 3 tab filter? Matlab gives you 5 coefficients for a 4 tab filter.
This is a didactic example, you can use it as template
Thanks
You are welcome!
that’s so useful my friend…. thank’s a lot…
You are welcome!
Tanks very much for your best code vhdl
And i need to more than this codes vhdl
Tanks
you are welcome, I appreciate your feedback
Your best
thank you!
Thanks Francesco! Compact and very useful codes!
Question: If the number of taps were generics, how can i generate the seperate process statements for the adder tree? can you give an example?
Thanks!
you have to add the process adder tree manually.
It is the best way to proceed.
Thanks for the reply!
I think it should be possible to realize a parametrized (Generic) adder tree using GENERATE statement.
All the best!
Can you have verilog code for FIR filter design, with hardware implementation.
Help me, Im not understood how filter working in real time, shall u give me some notes
I’m sorry, I deal only VHDL, you can translate the VHDL in Verilog
how shall i use modelsim with xilinxs as i dont have modelsim installed and from where i can get it
here you can find how to get a free modelsim license
https://surf-vhdl.com/how-to-get-free-modelsim-license-and-simulate-your-vhdl-code/
Can u plz help in writing vhdl code for 2- parallel fir filter…plzzzzzzzzz plzzz
you have to start with math parallelization of the filter,
then you can use the FIR template to implement the code
Sir where is test bench
just put your email in the box in the post. If you have problem in receiving the email, check your spam folder, sometimes the email is marked as spam
just put your email in the box
Please send me the test bench code sir
Sir, Can I get a test bench for this code?
you can find it here:
https://surf-vhdl.com/how-to-realize-a-fir-test-bench-in-fpga
just put your email and get the VHDL code
it give me this error Undefined symbol ‘resize’ what’is the solution please
Maybe you didn’t insert the library.
Btw, if you download the entire code it works.
hi dear,
I need some help on one project, I want to design FIR filter in FPGA using VHDL and connect it with any medium using high-speed serial interface to observer performance of FIR filter. can anyone help me in this regards?
BR:
Sarwan
Hi Sarwan,
take a look here
https://surf-vhdl.com/how-to-realize-a-fir-test-bench-in-fpga/
For the high-speed serial link, it depends on the FPGA you are using
hey I want to implement a low-pass FIR, how do I include the cut-off frequency? thanks
you have to design your filter with the classical digital design method.
Here you can find some example
https://www.mathworks.com/discovery/filter-design.html
https://help.scilab.org/doc/5.5.2/en_US/fsfirlin.html
Could you please elaborate on those 3 Lines of the Code
p_data <= signed(i_data)&p_data(0 to p_data'length-2);
for k in 0 to 1 loop
r_add_st0(k) <= resize(r_mult(2*k),17) + resize(r_mult(2*k+1),17);
end loop;
r_add_st1 <= resize(r_add_st0(0),18) + resize(r_add_st0(1),18);
Thank you
the function “resize” is used to extend the number of bit of its argument.
For instance
resize(r_mult(2*k),17)
extend to 17-bit the 16-bit multiplier output register extending the sign bit
Kindly can any one explain to me why in this line it’s Legnth – 2 (Which i though since the new entered data is a new 8 bits ,so it should be Legnth – 1)
p_data <= signed(i_data)&p_data(0 to p_data'length-2);
The “p_data” represents the filter data pipe.
In the example above the data pipe length is 4 registers of 8 bits.
The code can be rewritten as:
p_data <= signed(i_data)&p_data(0 to 2); since p_data'length = 4
can u plz provide us vhdl code for FIR Filter design by 4 bit multiplier.
send me an email, I will answer
what is your email ID sir?
Can you please suggest How to Implement FIR Filter in VHDL using 4bit multiplier???…………plzzzzzzz
just define the multiplier with 4 bit instead of 8
Hello,
I really liked this post. The post is one of the most helpful FIR filter tutorial on the internet.
I have one question about this code.
o_data <= std_logic_vector(r_add_st1(17 downto 8));
I believe this line of code divides the result by 128 (shifting). Why is that neccesary? I guess it is related to coefficients scaling, but I want to know why it is neccesary and how you come up with 128. Can you eloborate?
Thanks!
Hello,
This is the most helpful post about FIR filter on the internet! Thanks for sharing. I have one question about the VHDL code.
o_data <= std_logic_vector(r_add_st1(17 downto 8));
I believe this line of code divides r_add_st1 by 256. Why is that neccesary? I assume this has something to do with coefficients scaling/quantization. How do you come up with 256? Can you eloborate?
Thanks!
I will deal whit this topic in a DSP course, by know you can think about:
you are using fixed point arithmetics.
This means integer representation.
If you multiply two N x M bit the result is M+N bit, so if you want to come back to N bit you have to shift by M to the right.
Take a look here
https://surf-vhdl.com/how-to-divide-an-integer-by-constant-in-vhdl/
Sir/Madam
how can i implement the same 4 tap fir low pass filter in structural model! whether it is possible to call adders and multipliers programs for implementing 4 tap FIR Filter?
Hi,
you need to instantiate the component adder/multiplier.
Take a look on the link
https://surf-vhdl.com/vhdl-syntax-web-course-surf-vhdl/
You can follow my online course to understand how to do this.
Ciao
Hai sir,
How to compare the lowpass filter output from modelsim to lowpass filter from Matlab.
I generated filter coefficients fdatool from Matlab.
take a look here
https://surf-vhdl.com/how-to-realize-a-fir-test-bench-in-fpga/
how to verify the low pass filter from verilog hdl to matlab lowpass filter output.
check this
https://surf-vhdl.com/how-to-realize-a-fir-test-bench-in-fpga/
How to design a 3level DWT in VHDL??
you read this
https://download.atlantis-press.com/article/6291.pdf
Hi sir, I need the test bench of this code
thanks sir
Hi sir, The filter sampling frecuency is equal to the clock signal?
No, filter sampling frequency can be different
i use float core to convert my standard IEEE 32 bit float input to fixed point and use this code bud I dont know how to change the sampling frequency
what do you mean with “change the sampling frequency”?
Hi sir,
Can I use this filter for echo cancellation, if yes, what I need for more precision
if you want to implement it as a FIR, yes
i have designed afir filter in VHDL , want to use it in DSP how it can be?
I don’t understand your question, Can you reformulate?
sir/mam,
i want code for chebysev filter(IIR). Can you please provide me the code,its an urgent need for my final year project.
Is Multipication opearator (*),which you used in the line 56.Is it synthesizable?
yes. All the code in this post is fully synthesizable
In the test bench, you are using several coefficients -10, 110, 127, -20.
And the input is delta or a step of magnitude 127.
What is the equivalent float value above numbers if I want to do hand calculation using the formula of filter?
That is y[n] = b0*x[n] + b1*x[n-1] + b2*x[n-2] + b3*x[n-3]
Can you brief of how to convert filter coefficients to integers (fixed point) used in FPGAs
Thanks
you have to divide the positive number by 127 and the negative by 128
how we can add latch enable input in this code
for example we have 100 clock sample rate so every 100 clock , for one clock we have latch enable = 1
so i_data in every 100 clock latch and filter
please help meee
could you be more clear?
I need to perform a correlation algorithm, can you help me?
can i use this code ?
a correlator is a special case of a FIR, so you can easily adapt this code
hello sir, i want to design IIR chebyshev filter 1 and implementation on FPGA,