CNN Kernel implementation in VHDL

In the last years, Machine Learning (ML), Artificial Intelligence (AI), Deep Learning are topics that are driving electronic device development.

ML and AI are starving in computational power.

The FPGA, mainly the modern FPGAs, are used in ML/AI since they can implement a lot of convolutional engines inside due to the intrinsic parallel architecture.

The CPUs and GPUs are processing units that can have (especially GPU) a lot of computational general purples engine inside.

A CNN kernel is basically a matrix multiplication. The faster a device can perform such multiplication, the faster the device can “think”. This is an intrinsic parallel architecture so which is the best device that can be used to implement such architecture?

Yes, the FPGA!

The modern FPGA implements a lot (in the order of thousand) Multiply and Accumulate (MAC) engines inside.

For instance, high-end FPGA such as the Kyntex UltraScale KU13P has 3528 MACs inside or the Virtex Ultrascale up to 12288 MACs.

The Intel Stratix MX 2100 implements 7920 MACs or in the Intel DX 2800, there are 11520 MACs inside!

Well, a lot of stuff…

think about how many multiplications you can perform for each clock cycle!

No GPU can win against such computational power!

But… the power is nothing without control!

First of all, if you want to take advantage of such MACs you need to understand about Digital Signal Processing (DSP).

As you can see in the FPGA datasheet, all these devices are optimized to handle fixed-point numbers.

Ok, in the modern FPGA you can use also floating-point representation, but you are wasting a lot of processing (and dissipation) power without taking real advantage from these devices!

Well, let’s understand how to implement a CNN kernel.

CNN Kernel implementation

The first thing to do when work with CNN, is to quantize the network coefficients. Generally, we can use INT8 quantization. I mean 8-bit quantization both for the weights and the input to the network. The modern FPGA can handle 2 or more multiplication per single MAC engine. In this case, the number of MACs above can be doubled!

a typical convolutional kernel is:

where N = 3 or 5 or more.

This is a typical matrix multiplication.

We can implement such a kernel in different ways, depending on how fast we want to compute the result.

I mean, we can use a single MAC and compute the output after M clock cycles where M=N*N

If we parallelize the operations, we can reach a real-time computation, I mean, one output per clock cycle.

Of course, the implementation depends on the data rate we need to guarantee and on how much MACs are available on our FPGA.

Let’s see a CNN kernel implementation for N=3

As you can see the we can implement the matrix multiplication as 3 FIR of three taps per filter. On the other hand, we can see a FIR as scalar product of two vectors:

coefficient vector by data pipe vector.

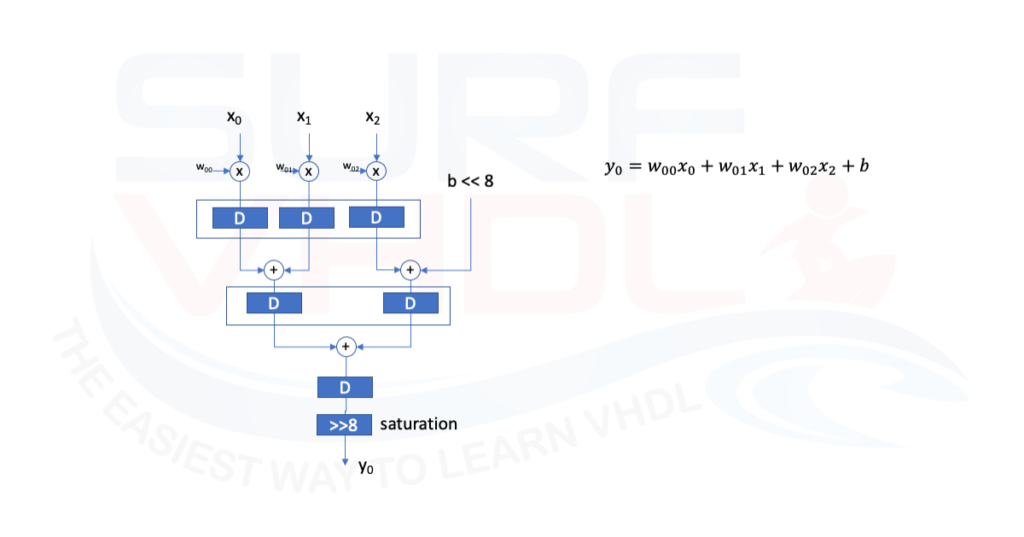
In this example, is missing the output section of a CNN kernel: the activation function.

The activation function can be easily implemented as a LUT. You can see an example in this post.

Now, we know how to implement a FIR filter.

If not, just take a look to this post.

As stated before, we will use INT8 quantization, I mean, the coefficient and the input are 8 bit wide.

The internal operations are computed at full dynamic, in this example, the output will be the 8 MSB of the full dynamic operation.

When we multiply two numbers NxM the result is N+M bit. In this case input and coefficient are 8 bit, so the result will be 16 bits.

So if we want to add the constant b at this stage, we need to take into account the increment of the dynamic due to the multiplication operation, in this case, 8 bit due to the coefficient w.

Then we have the increment of dynamic due to the addition operation.

Even in this case we need to cut the output dynamic to 8 bits. We will use the same strategy used for the FIR implementation. I mean we will shift by a certain number of bit and then saturate at 8 bits.

The number of right shifts depends on the coefficient value and input value. this is a very delicate point and requires simulation at system level.

You can perform some Matlab simulation, to understand the optimum amount of shift you need to perform. In this example we can assume a shift by 8 and then saturation.