Why Galois field
The Galois fields are mainly used in cryptography and error correction algorithm.
If you never deal with Galois field, at the beginning the topic could seem very hard to understand. In this post we want to address the galois field theory from the practical application point of view.
We will review:
- the Galois arithmetic notation, just to understand how to interpret the equation
- add/sum operation in Galois field
- multiplier in Galois field
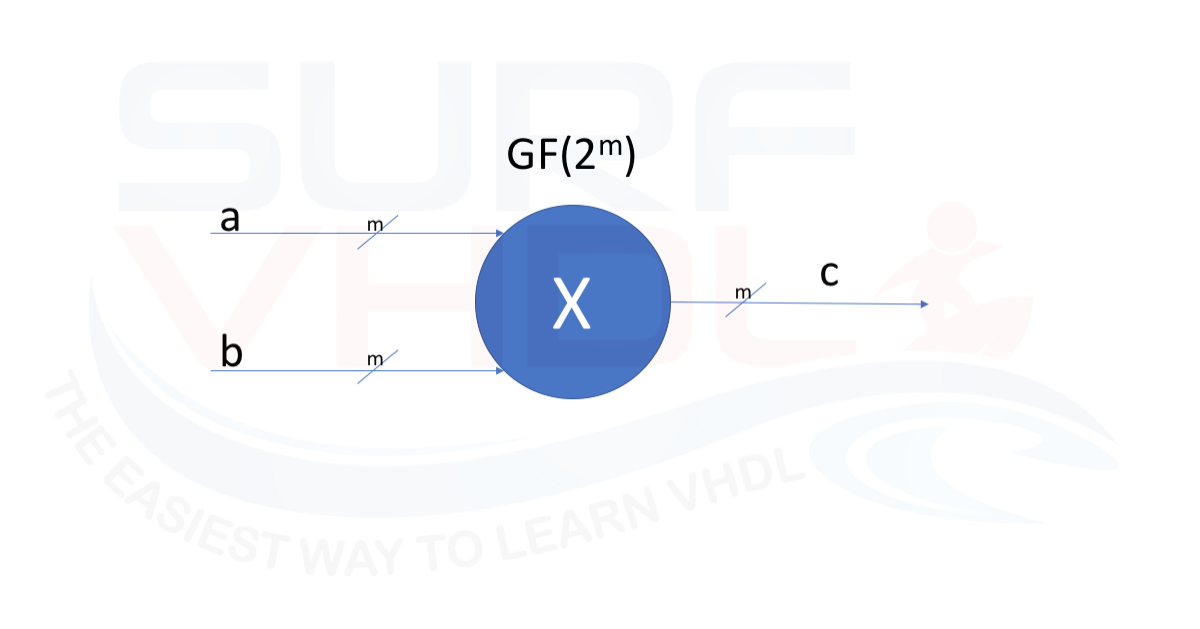
the third point maybe is the most difficult to understand.
It might put noses out of joint after reading this post because I will not be very rigorous in the representation of the theory of the Galois fields. This post wishes to give you a practical implementation starting point for your VHDL design using Galois arithmetic.
I put a lot of references at the bottom of this post that will help you to go deeper in the Galois field theory if you are really interested in it.
Galois field notation
Before starting let’s review some arithmetic notation:
GF(Pm) represents a Galois field of Pm element. Here we will consider P=2.
A primitive polynomial p(X) is defined to be an irreducible binary polynomial of degree m which divides X^n+1 for n = P^m-1 = 2^m-1 and which does not divide X^i+1 for i<n.
Once a primitive polynomial p(X) is found, then the elements of the Galois field can be generated.
At this link, you can find an example of a primitive polynomial
Here I don’t want to go deeper in the Galois field theory, so let’s make an example:
p(x) = 1 + x + x^4
is a primitive polynomial for GF(2^4) = GF(16)
another primitive polynomial for GF(16) is
p(x) = 1 + x + x^2 + x^3 + x^4
Another notation for p(x) polynomial is the vector representation:
p(x) = x^4 + x + 1 = 10011 = 19dec = 0x13
Addition and Subtraction in GF(2^m)
In GF(2^m) field addition and subtraction are totally equivalent. The addition operation is performed by XOR operator. In this case, the vector representation of a polynomial is very helpful:
For example, if we want to add two polynomials in GF(16):
G1(x) = x^3 + x^2 +1; G2(x) = x^3 + x
In vector representation we can write:
G1(x) => 1101 G2(x) => 1010
So G1(x) + G2(x) will be
1101 + 1010 = ------ 0111
G1(x)+G2(x) = x^2 + x + 1
Since 2*X^3 = 1 XOR 1 = 0
We will obtain the same result for G1(x) -G2(x)
Multiplication in GF(2^m)
In the previous section, we saw that the add/sub operation in the Galois field is very simple since we can perform it as bitwise XOR. The multiplication is a little bit more complicated since the multiplication of two polynomial g(x) and f(x) is defined as follow:
m(x) = (g(x) * f(x)) mod(p(x))
The result of a multiplication is the reminder of the multiplication result f(x)*g(x) divided by the primitive polynomial of the field.
The bitwise multiplication is performed using AND operator.
For example:
f(x) = (a3*x3 + a2*x^2 + a1*x1 + a0) g(x) = (b3*x3 + b2*x^2 + b1*x1 + b0) f(x) *g(x) = (a3*x3 + a2*x^2 + a1*x1 + a0) * (b3*x3 + b2*x^2 + b1*x1 + b0) = (b3*x3 + b2*x^2 + b1*x1 + b0) a0 + (b3*x3 + b2*x^2 + b1*x1 + b0) a1 x^1 (b3*x3 + b2*x^2 + b1*x1 + b0) a2 x^2 (b3*x3 + b2*x^2 + b1*x1 + b0) a3 x^3
As clear is the classical multiplication algorithm where the second row is shifted right by 1, the second by 2 and so on.
the “*” operator is omitted for sake of visualization.
In a practical example:
a3 = 1, a2=0, a1=0, a0 =1 => f(x) = 1001 = 9 dec = 0x9
b3 = 1, b2=1, b1=0, b0= 1 => g(x) = 1101 = 13dec = 0xD
1101 *
1001 =
--------------
1101 +
0000 +
0000 +
1101 =
--------------
1100101 = x^6 + x^5 + x^2 + 1 = 101 dec = 0x65
The results do not belong to the GF(16) so we need to perform the division by the primitive polynomial
x^2 + x
x^4 + x + 1 |_____________________________________________
x^6 + x^5 + x^2 + 1
x^6 + x^3 + x^2
--------------------------------------------
0 x^5 + x^3 + 1
x^5 + x^2 + x
--------------------------------------------
x^3 + x^2 + x + 1 = 15dec = 0xF
Matlab / Octave example code
a = gf([9],4,19); b = gf([13],4,19); m = a*b =15
Implement Multiplier in GF(2^m) using VHDL
It is possible to demonstrate that the modulo operation can in GF(P^m) be implemented using LFSR approach. In this post, you can find an LFSR implementation in VHDL. Here below is reported the VHDL function that implements a Galois multiplier in GF(2^8) using the primitive polynomial
p(x) = 1 + x^2 + x^3 + x^4 + x^8 = 100011101b = 285dec
function mult285 (v1, v2 : in std_logic_vector) return std_logic_vector is
constant m : integer := 8;
variable dummy : std_logic;
variable v_temp : std_logic_vector(m-1 downto 0);
variable ret : std_logic_vector(m-1 downto 0);
begin
v_temp := (others=>'0'); -- 1 + x^2 + x^3 + x^4 + x^8
for i in 0 to m-1 loop
dummy := v_temp(7);
v_temp(7 ) := v_temp(6 );
v_temp(6 ) := v_temp(5 );
v_temp(5 ) := v_temp(4 );
v_temp(4 ) := v_temp(3 ) xor dummy;
v_temp(3 ) := v_temp(2 ) xor dummy;
v_temp(2 ) := v_temp(1 ) xor dummy;
v_temp(1 ) := v_temp(0 );
v_temp(0 ) := dummy;
for j in 0 to m-1 loop
v_temp(j) := v_temp(j) xor (v1(j) and v2(m-i-1));
end loop;
end loop;
ret := v_temp;
return ret;
end mult;
The Matlab / Octave code to verify the result is:
A = gf([34],8,285); B = gf([55 12 42 231 2 254 1 87],8,285); C = A.*B The result is: 192 133 125 98 68 87 34 156
Simulation and Layout of VHDL multiplier if GF(2^8)
In Figure 2 is reported the VHDL simulation of the mult285 Galois multiplier VHDL code:
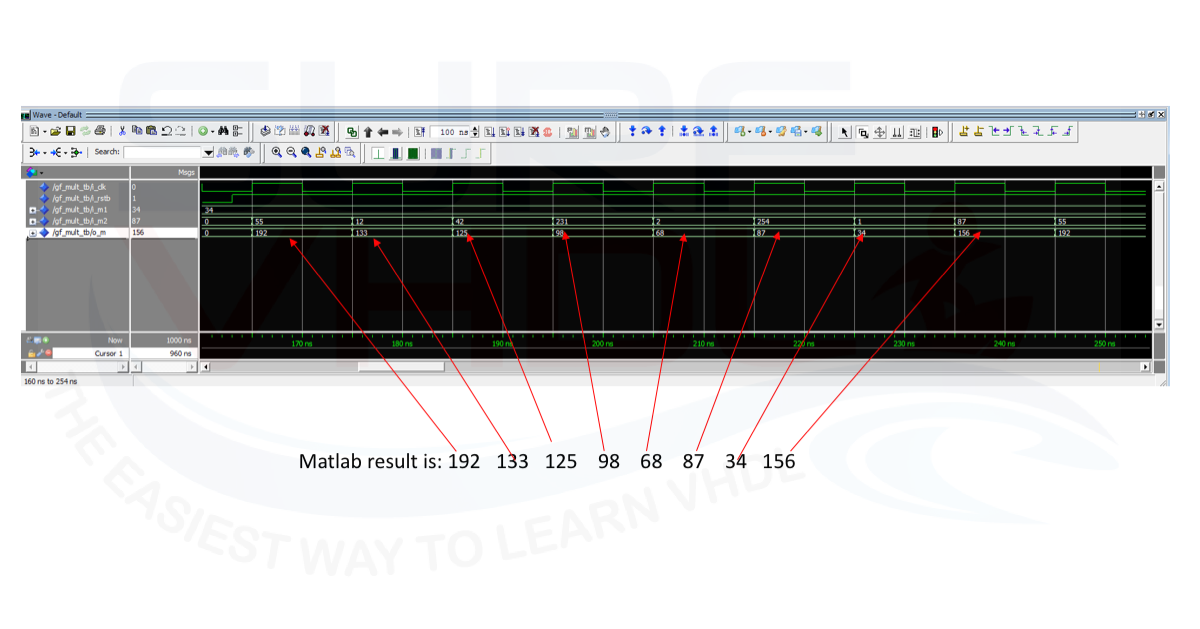
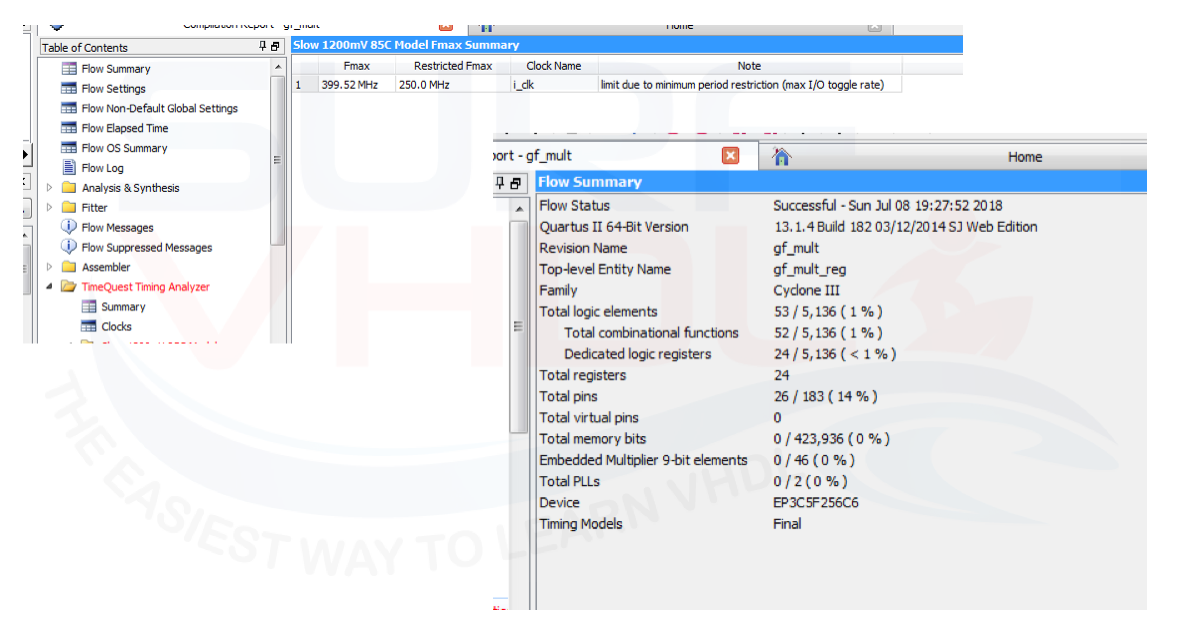
Figure 3 reports the layout result of the VHDL implementation of the Galois multiplier. In order to evaluate the clock frequency, input and output Flip/Flop have been added to the VHDL design. The 24 registers reported in the summary are relative to 2×8 = 16 input registers plus 8 output registers. On a Cyclone III FPGA the timing analysis reports 400 MHz
Conclusion
In this post, we introduced the Galois field arithmetic.
The ADD/SUB operators are reduced to XOR operation, multiplier operation is implemented as XOR and AND operation. The result is reduced using the primitive polynomial relative to the Galois field.
A generic VHDL implementation has been proposed. The VHDL code for the Galois multiplier can be simply modified to perform multiply operation in different Galois field and different primitive polynomials.
References
[2] https://www.mathworks.com/
[4] https://www.gnu.org/software/octave/
[5] https://en.wikipedia.org/wiki/Finite_field
[9] “Reed-Solomon error correction, R&D White Paper WHP 031”, C.K.P. Clarke
[11] “Reed Solomon Codes Explained” Tony Hill, 8th May 2013, v1-0
[12] “VHDL Implementation of Reed Solomon Improved Encoding Algorithm”
[13] “VHDL IMPLEMENTATION OF REED-SOLOMON CODING”, SUBHASHREE DAS
[16] “Galois Field in Cryptography”, Christoforus Juan Benvenuto
Nice work.
Thank you for your feedback!
Wow, thank you for this short and concise course
you are welcome!
Thank you very much. Very concise and clear.
Keep up the good work!
thank you!
“function mult285 (v1, v2 : in std_logic_vector) return std_logic_vector is”
is there something after is??? because is doesnt appear to me. Thanks
all the code is in the post.
after “is” the code continues on a new line.
I don’t understand your question
how do i implement this for gf(2^128)?
how do i implement this for gf(2^128) with irreducible polynomial x128 + x7 + x2 + x + 1.