How to Quantize FIR Coefficient

Fixed vs floating point representation

When we use FPGA, we need to deal with fixed-point arithmetic. Even if new FPGA like Intel Stratix 10 implements floating-point multiplier, if we need to implement Digital Signal Processing (DSP) in FPGA we have to use fixed-point arithmetic.

Many people have serious problems dealing with fixed-point binary representation or quantization of floating point value in fixed-point.

In this post, I explained how to divide a number for a constant in VHDL. Of course, you need to have the basic of binary number representation that you can find in this post.

Fixed-point representation introduction

In VHDL generally, we use binary signed fixed-point number representation. Using the signed binary representation, we can take advantage of the standard library for the

• addition
• subtraction
• multiplication

Just to be clear, you can use also unsigned binary number representation, but if you are implementing a DSP architecture is very likely that you need to deal with positive and negative numbers.

In signed fixed-point representation we need to define the number of bits we are using to represent our number.

 

For example, if we use 8 bit, we can represent all the integer number in the range -128<= Number <=+127

i.e. -2^(N-1) <= Number <= +(2^(N-1))-1

where N=8.

in the signed representation the negative numbers one more than the positive.

If we deal with unsigned binary number the range will be

Number <= +(2^N)-1

For example, for 8-bit number 0..255

---

Fixed-point representation of an FIR coefficient

What we are going to say in this section is valid for any kind of binary quantization.

When we need to quantize the impulse response of an FIR filter we need to:

• set the number of bits to represent the coefficient
• scale the floating point of the impulse response w.r.t. the maximum value
• convert the scaled coefficient to a fixed-point value

You can use MATLAB script, Scilab script, Excel or your calculator to implement these steps.

Here below the commands to quantize your floating point FIR impulse response (coefficient) in Scilab. The Command can be used in MATLAB too.

 N = 8; 
 MaxPos = (2^(N-1))-1; 
 MaxNeg = (2^(N-1));

h  = [

   0.02674
  -0.01668
  -0.07822
   0.26686
   0.60294
   0.26686
  -0.07822
  -0.01668
   0.02674];

hNorm = h./max(h)

ptrNeg = find(hNorm<0);

hQ = hNorm .* MaxPos

hQ(ptrNeg) = hNorm(ptrNeg) .* MaxNeg

hQ = round(hQ)

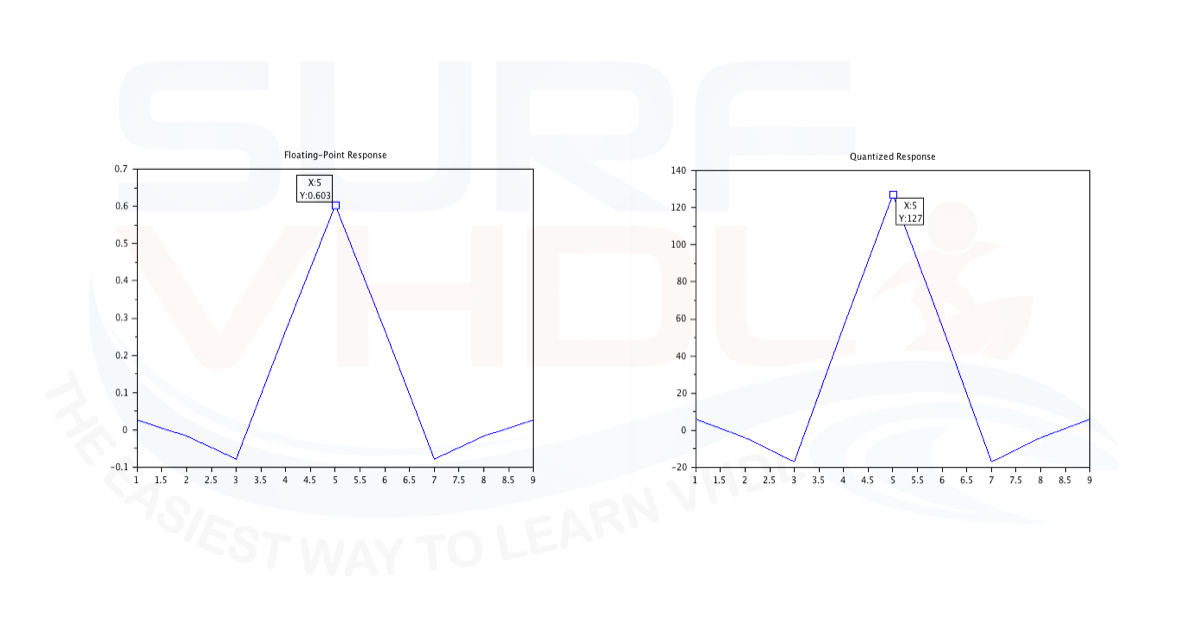
plot(h)
title('Floating-Point Response')

figure
plot(hQ)
title('Quantized Response')

In Figure 1 the floating-point and quantized version of the FIR impulse response

In line 17 we are normalizing the impulse response between -1..+1.

Notice that we are assuming that the maximum value is positive.

In line 19 we find all the index of negative values.

In line 21 we are quantizing for the positive values multiplying the normalized impulse response by the maximum positive value.

In line 23 we overwrite the negative quantized values

In line 25 quantize the coefficient in fixed-point values by rounding the floating-point version.

---

 

Conclusion

In this post, we learn how to quantize in fixed point the impulse response of an FIR. The quantization has been implemented using Scilab (compatible with MATLAB) commands.

 

References

[1] https://www.altera.com/products/fpga/stratix-series/stratix-10/overview.html

[2] https://www.mathworks.com/

[3] http://www.scilab.org