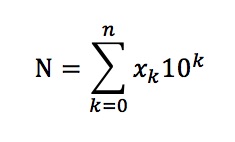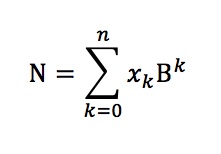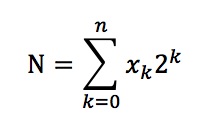In this post, we want to give an overview to binary number representation for negative numbers. Will be review three different representations for the negative number.
To understand binary numbers, we can start recalling elementary school math.
When we first learned about numbers in the decimal system, the number where organized into columns:
H | T | O 4 | 3 | 2
such that
- “H” is the hundreds column,
- “T” is the tens column,
- “O” is the ones column.
So the number “432” is 4-hundreds plus 3-tens plus 2-ones.
Generally speaking a base 10 number is defined:
for the example above will obtain:
432 = 4*10^2 +3*10^1+2*10^0;
In a generic base B a number “N” is defined:
With x=0,1..B-1;
In fact in base 10, x can be 0,1..9;
In base 3, x can be 0,1,2
In base 2, x can be 0,1
After this brief review, let’s go to understand better the binary representation. If we need to represent the integer from 0 to 7, it is clear that we need at least 3 digits or bit. This representation respects the formula:
With xk= 0,1
INTEGER BINARY
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111
The numerical operation follows the same rules of basic math learned in elementary school.
Ex:
1 Carry 010 + (2d) 011 = (3d) 101 (5d)
i.e 2+3=5
This is binary representation for a positive number.
What if the number is negative?
In this case there are three different solutions for the binary representation:
- Sign + magnitude
- 1’complement
- 2’complement
In all the three representations, the MSB (Most Significant Bit) of the binary number represents the sign bit.
Let’s see in detail the differences between the three binary representations.
Sign + Magnitude
The simplest solution is Sign + Magnitude.
For N-Bit binary number, the N-1 bit represent the magnitude, the N-th bit (MSB), represents the sign bit
For example, if we have 3-bit binary number:
010b = +2d 110b = -2d
INTEGER BINARY
+3 011
+2 010
+1 001
+0 000
-0 100
-1 101
-2 110
-3 111
As clear the representation has two different values for zero: positive zero (000) and negative zero (100).
1’complement
The 1’complement negative representation is simply obtained with bit complement of the corresponding positive value.
a_1c <= not a; 010b = +2d => negative: not(010) = 101b = -2d
INTEGER BINARY
+3 011
+2 010
+1 001
+0 000
-0 111
-1 110
-2 101
-3 100
Even in the case the zero value suffers of double representation: “000” and “111”
The 2’ complement representation
The 2’ complement representation resolves the problem for the zero value:
Negative value in 2’ complement representation is: (2^N)-v
Where v is the positive value we want to be converted to negative one, and N is the number of bits:
For example:
-2d will be converted in: 2^3 - 2 = 8 - 2 = 6d =
110b
INTEGER BINARY
+3 011
+2 010
+1 001
+0 000
-1 111
-2 110
-3 101
-4 100
In this case the numerical representation in unbalanced. The negative values contain one value more the positive values. The zero has only one representation.
The 2’complement representation simplifies all the numerical operation in binary arithmetics, in fact if we need to perform the subtraction:
A-B
We need to perform
A+(-B)
Example:
3-1 = 3+(-1) 11 carry 011 + ( 3d) 111 = (-1d) 010
Of course we have the same result with 5-bit representation:
1111 carry 00011 + (3d) 11111 = (-1d) 00010
As rule of thumb, in 2’complement representation, the number zero is represented always with all bit set to “0”, the number “-1” is represented with all bit set to “1”. In 2’complemnt using N-Bit, we can represent the following range: –2^(N-1) .. 2^(N-1)-1 For example:
N=8 => -2^7 ... 2^7-1 = -128 .. +127
N=3 => -2^2 ... +2^2-1 = -8 ... +7
Sign extension
As clear we will use always 2’complement representation in digital arithmetics. Every time we perform an arithmetic operation we need to know if the operands are
Signed or unsigned, i.e. if the MSB shall be interpreted as the sign bit.
In case of signed operation, if the operands are represented with a different number of bit, we need to handle with care the sign bit.
Arithmetic operation review.
The number of bit of the result of a binary arithmetic operation can be different from the number of bit of the input operand and depends on the operation.
In the following section, we will see few example for addition, subtraction and multiplication. As general rule, if we have two numbers A of N-Bit, B of M-Bit the bit increment for the arithmetic operation result will be:
- ADD/SUB: max(N,M) + 1;
- MULT: N+M;
ADD/SUB
C=A+B;
with A and B of N bit the number of bit of C can be up to (N+1)
Example unsigned:
A=3; B=2; N=2 unsigned
1 carry 11 + (3d) 10 = (2d) 101 (1d)
The result should be C = 5; result width is of N+1=3 bit width. If we don’t handle the carry the result “wrap around”
Pay attention for signed result
Example signed:
A=3; B=2; N=3 signed
1 carry 011 + (+3d) 010 = (+2d) 101 (-3d)
The result should be C = 5; results is N+1=4 bit width. If we don’t handle the carry the result “wrap around” and became negative
MULT
C=A*B;
with A of N bit and B of M bit the number of bit of C will be (N+M).
The multiplication algorithm is the well-known shift and add:
Example unsigned:
A=3 (2 bit unsigned); B=7 (3 bit unsigned);
111 x (+7d) 11 = (+3d) 111 + 111- = 10101
C=21d is represented with 5 bit=3+2
A=5 (3 bit unsigned); B=2 (2 bit unsigned);
101 x (+5d) 10 = (+2d) 000 + 101- = 1010 (+10d)
Pay attention on signed multiplication
A=-2 (4 bit signed); B=5 (4 bit signed);
1110 x (-2d)
0101 = (+5d)
11110 + (sign extension)
0000- + (sign extension)
11110-- = (sign extension)
1110110 (-10d)
Sign extension
The sign extension rule for 2’complement representation can be summarized as follow:
- If the number is unsigned, no sign extension are required.
- If the number is signed, the sign extension is implemented propagating the bit sign toward the MSB
Example:
N bit 3;
-3d = 101
Sign extension to N-bit= 6: -3d = 111101
Resize Function
In VHDL, the simple way to perform the sign extension is to use “resize” function provided by the numeric_std library. The “resize” function tells the simulator/synthesizer to extend the sign. In this case, the sign extension is performed in the best way for the target technology.
In the first example the “resize” function call is performed on “signed” signal.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity resize_example is generic( N : integer := 8; M : integer := 10); port ( i_val : in signed(N-1 downto 0); o_val : out signed(M-1 downto 0)); end resize_example; architecture rtl of resize_example is begin o_val <= resize(i_val,M); end rtl;
Resize function Example 1
The second example is totally equivalent to the first one. In this case, we need to explicit to the simulator/synthesizer how to treat the signal of std_logic_vector type. The type casting informs the simulator/synthesizer that we need to perform a sign extension on signal “i_val”.
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity resize_example is generic( N : integer := 8; M : integer := 10); port ( i_val : in std_logic_vector(N-1 downto 0); o_val : out std_logic_vector(M-1 downto 0)); end resize_example; architecture rtl of resize_example is begin o_val <= std_logic_vector(resize(signed(i_val),M) ); end rtl;
Resize function Example 2
When possible, it is more efficient to use the native function instead of writing redundant VHDL code.
Another way to implement sign extension is given below:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity resize_example is port ( i_val : in std_logic_vector(8 downto 0); o_val : out std_logic_vector(10 downto 0)); end resize_example; architecture rtl of resize_example is begin o_val <= i_val(8)&i_val(8)&i_val; end rtl;
Resize function Example 3
In the last example, the sign extension is performed “by hand”. The code is less portable. The VHDL-RTL code above is fully-synthesizable, and you can take as a reference all the three example above. As a rule of thumbs, you should always use all the predefined function before trying to reinvent the wheel writing your custom code. The predefined functions, when available, guarantee always the best hardware implementation and your VHDL code will be technology independent.
If you find this article useful, please share the link with your friend.
[social_sharing style=”style-7″ fb_like_url=”http://bit.ly/BinaryNumberRepresentation1″ fb_color=”light” fb_lang=”en_US” fb_text=”like” fb_button_text=”Share” tw_text=”Hi, here you can find a post for Binary Number Representation” tw_lang=”en” tw_url=”http://bit.ly/BinaryNumberRepresentation4″ tw_name=”@SurfVHDL” tw_button_text=”Share” g_url=”http://bit.ly/BinaryNumberRepresentation3″ g_lang=”en-US” g_button_text=”Share” linkedin_url=”http://bit.ly/BinaryNumberRepresentation2″ linkedin_lang=”en_US” alignment=”center”]
If you need to contact us, please write to: surf.vhdl@gmail.com